| STATIC: Strain Types |
static allows the user to select
from a pre-defined set of lattice
types, or to define an arbitary lattice. This choice is
made in the subroutine setlat.f.
In many cases, however, you may want to start with a basic lattice type, say a face-centered cubic (fcc) lattice, and then distort the lattice. For example, you might want to calculate the elastic constants of a crystal based on the tight-binding parametrization.
setlat.f allows you to generate an arbitrary
strain, or to select one of several defined strain types. What
we mean by strain is defined in many solid-state theory
textbooks, including Kittel and Ashcroft & Mermin. In
general, a strain is represented by a strain tensor, which
transforms a set of primitive lattice vectors.
To see this, let's start with an arbitrary primitive lattice:
| ( |
|
) | = | ( |
|
) | . | ( |
|
) | (1) |
where X, Y, and Z are unit vectors pointing along the Cartesian axis and the parenthesis surround matrices.
A general strain will bend and perhaps change the length of the unit vectors. Since a rotation of the coordinate axis does not change the total energy of the system, we can restrict ourselves to non-rotating strains. These strains can be represented by a symmetric strain matrix, which has the effect of changing the relationship between X, Y, and Z. This matrix is usually expressed in terms of ei, the strain coefficients:
| ( |
|
) | = | ( |
|
) | . | ( |
|
) | . (2) |
The strain matrix changes the unit vectors in (1) to the primed vectors of (2). Thus the new lattice can be described as:
| ( |
|
) | = | ( |
|
) | . | ( |
|
) | . | ( |
|
) | . (3) |
By Hook's law, if the strains ei are small, the change in the energy of the lattice is proportional to the square of the strains:
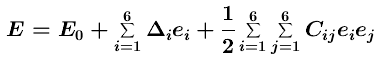 |
+ O[e3] . (4) |
The linear terms vanish when we are at equilibrium, or if the strain causes no change in the volume of the crystal. Otherwise, the "deltas" are related to the strain on the crystal, and the Cij are the elastic constants. Since the strain matrix (2) is symmetric, we can assume the Cij tensor to be symmetric, too:
Cij = Cji . (5)
There are thus 21 independent elastic constants. This number can be reduced by symmetry. For example, in a cubic crystal, such as copper, niobium, or diamond, symmetry demands that, e.g. C11 = C22. In fact, only three independent elastic constants remain, so that (4) reduces to
E = E0 + ½ C11 [ e11 + e22 + e33] + C12 [ e1e2 + e2e3 + e3e1] + ½ C44 [ e44 + e55 + e66] + O[e3] . (6)
(Equation (6) assumes that we start from equilibrium, i.e., there are no stress terms.)
It is obvious the several linear combinations of elastic
constants and strains will occur frequently. They occur so
frequently, in fact, that the static program has several
pre-defined strains included in the code. These strains are
defined in the setlat.f subroutine. The table
below describes the strains already defined. Any user can of
course add additional strains by editing setlat.f.
In addition, as can be seen in option zero, a general strain
can be entered.
In each entry of the table, only the listed ei are non-zero. The column labeled "Parameters Entered" indicates the actual input expected by the code, in the order it should be given. The remaining column labels should be self-explanatory, except for column 5. There, "QE/V" means "the quadratic part of the energy (4) divided by the volume."
| Index | Strain | Parameters Entered | Volume Conserved? | QE/V | Notes |
|---|---|---|---|---|---|
| 0 | None | Yes | 0 | No strain: no additional strains are imposed on the lattice | |
| 1 | All ei | All ei | Not in general | See Equation(4) | General arbitrary strain |
| 2 | e1=[(1+x)/(1-x)]½-1 , e2=[(1-x)/(1+x)]½-1 | x2 | Yes | ½ (C11 + C22 - 2 C12) x2 + O[x4] | Use one of these forms when it is known that E(-x) = E(x). See, e.g., Example IV. |
| -2 | e1 = x , e2 = -x , e3 = x2/(1-x2) | ||||
| 21 | e1=[(1+x)/(1-x)]½-1 , e2=[(1-x)/(1+x)]½-1 | x | Yes | ½ (C11 + C22 - 2 C12) x2 + O[x3] | Same as 2 or -2, except for use in the case E(x)<>E(-x) See Example X (C11-C22). |
| -21 | e1 = x , e2 = -x , e3 = x2/(1-x2) | ||||
| 3 | e1=e2=[(1+x2/4] ½-1 , e6=x | x2 | Yes | ½ C66 x2 + O[x4] | Use one of these forms when it is known that E(-x) = E(x). See, e.g., Example V. |
| -3 | e3 = x2/(4-x2) , e6 = x | ||||
| 4 | e1 = e2 = (1+x) -1/3 e3 = (1+x)2/3 | x | yes | 1/18 (C11 + C22 + 4 C33 + 2 C12 - 4 C13 - 4 C23) x2 + O(x3) | ``Bain Path'' for fcc and bcc Crystals. See Example VI. Also see the E(c/a) at fixed volume in the hcp elastic constants tutorial |
| 5 | e1,2,3 = (1+x)/(1+3x)1/3 -1 e4,5,6 = 2x/(1+3x)1/3 | x | yes | 2 (C44 + C55 + C66) x2 + O(x3) | Analog of the ``Bain Path'' along the <111> direction. |
| 6 | e3 = ¼ x2 e4 = x | x2 | yes | ½ C44x2 + O(x4) | E(-x)=E(x) in a hexagonal lattice. See Example X (C44). |
Suggestions on how to use these strains can be found in the examples section of this manual.
static Home Page Introduction Installation List of Files Usage Input Files Output Files Trouble Shooting Appendix
Current URL: http://esd.cos.gmu.edu/tb/static/straintype.html