Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example X

Change in energy as a function of c/a at fixed Volume

In the fixed c/a calculation we looked at the energy as a function of the volume, V, at a fixed c/a ratio. In this section we'll turn that around and look at E(c/a) at fixed volume.

What do we get out of this? The answer lies in the theory of elasticity, to which we give short shrift here, and a bit longer explanation in a review article. Basically, if we work at constant volume, then changing the c/a ratio from the equilibrium value of (c/a)₀ to c/a without changing the volume requires the strain parameters e_i to obey the equations

e₂	=	e₁
(c/a)/(c/a)₀	=	(1+e₃)/(1+e₁)	(1)
(1+e₁)² (1+e₃)	=	1

If we define the relative change in c/a as

z = (c/a)/(c/a)₀ - 1 , (2)
then (1) requires

e₁ = e₂ = (1+z)^-1/3 - 1 = -1/3 z + O(z²)

(3)

e₃ = (1+z)^2/3 - 1 = 2/3 z + O(z²)

Then as a function of z, the energy change can be related to the elastic constants by

E(z) = E₀ + 1/9 V₀ [ C₁₁ + C₁₂ + 2 C₃₃ - 4 C₁₃ ] z² + O(z³) . (4)

Looking at our predefined strains table, we see that the situation described here is just strain type 4, except that we've written z instead of x. It's also the same strain we used in computing a Bain Path.

The path we want to take is then clear: we set up a SKIN file for an undistorted lattice starting with the ground state structure of our TB parameters for titanium, strain the crystal for several values of z (uh, x), and compute the elastic constant from

C_zz = C₁₁ + C₁₂ + 2 C₃₃ - 4 C₁₃ = 9/2 E''(z = 0)/V₀ . (5)

The SKIN file required for this job is stored in work/czz/SKIN . Since we still have not changed symmetry, it uses the same space group file (work/spcgp1.hcp), k-point mesh ( work/kmesh.194), and tight-binding parameters ( work/ti_par). The only thing new about the file is the response to the strain:

Mode=3               (Calculate energy only -- no pressure)
0.005  0.500         (T_{Fermi}, Eigenvalue cutoff for P calculation)
../ti_par
Titanium HCP (A3) -- Fixed Volume = 220.088 Bohr^3
 1.61326030 -0.050   (We'll use the label to indicate c/a and strain)
 0.00                (Electrons in addition to nominal Ti charge (=4/atom))
-3                   (hexagonal lattice, read in V and c/a)
 220.088  1.61326030 (V in Bohr^3 and c/a)
 4                   (c/a strain)
-0.050               (the strain factor)
 2                   (Atoms in the unit cell)
 4 4 4               (Neighbor search cutoff indices)
F                    (Logical variable -- no internal displacements)
1 0.33333333333333333 0.66666666666666667 0.25 0 0 0   (Atom 1 in lattice coord.)
1 0.66666666666666667 0.33333333333333333 0.75 0 0 0   (Atom 2 in lattice coord.)
NEWSYM=T             (Generate new set of k-points)
LATTIC=4             (Lattice type / Next is spacegroup file name:)
../spcgp1.hcp
ILAT=T               (Space group file in lattice Coordinates)
-1313                (Read k-point generation information from file)
../kmesh.194

The strain type is ``4'', and we enter strain factors which range from -0.05 to +0.05. The final work/czz/SKENG file looks like this:

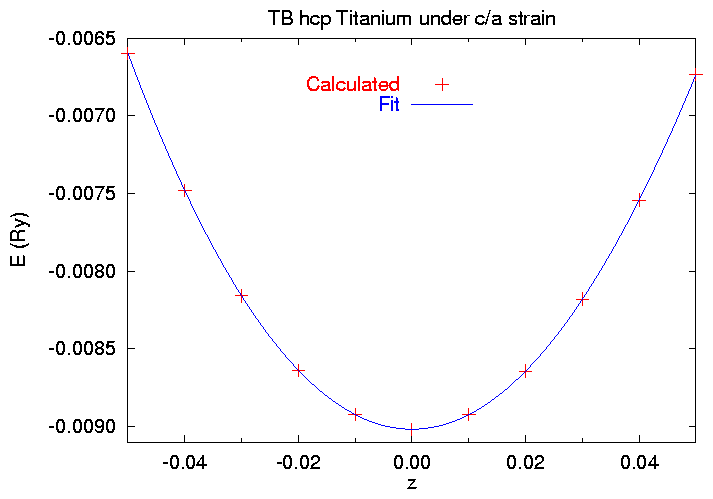
$ cat SKENG
 1.61326030 -0.050    220.088000     .129360839    -.006598475
 1.61326030 -0.040    220.088000     .129307485    -.007481490
 1.61326030 -0.030    220.088000     .129184366    -.008159764
 1.61326030 -0.020    220.088000     .128996025    -.008638850
 1.61326030 -0.010    220.088000     .128754153    -.008923907
 1.61326030 +0.000    220.088000     .128472502    -.009018141
 1.61326030 +0.010    220.088000     .128162422    -.008923908
 1.61326030 +0.020    220.088000     .127830874    -.008643724
 1.61326030 +0.030    220.088000     .127479045    -.008181259
 1.61326030 +0.040    220.088000     .127103646    -.007542400
 1.61326030 +0.050    220.088000     .126700829    -.006735028

Since we know V₀ and E₀, and we know that z=0 is the equilibrium point, we can use gnuplot to fit this data to the polynomial

E(z) = E₀ + 1/9 V₀ z² [ C_zz + z ( A + z ( B + z C))] , (6)

where C_zz is defined in (5) and A, B, and C are higher order elastic constants. When we run the fitting script we get

$ gnuplot !$
gnuplot czzfit.gnu
Starting from v0 = 220.088 and e0 = -0.009018141
Change if appropriate
Press  to continue
[Fitting information deleted, see work/czz/fit.log]
C_{zz} = 567.036295923323 GPa
Press  to quit
$

and the fit looks like this:

So the result of this section is that we've found

C_zz = C₁₁ + C₁₂ + 2 C₃₃ - 4 C₁₃ = 567.0 GPa

Go back to the Example X home page.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

static Home Page Introduction About Version 1.11 Installation List of Files Usage Input Files Output Files Trouble Shooting Appendix

Return to the static Reference Manual.