Theory
The last elastic constant we want to calculate is C44. It is the most difficult constant to calculate for an hcp crystal. The simplest strain I found is strain type 6 in the predefined strain table:
e4 = x ; e3 = + ¼ x2 ; e1,2,5,6 = 0 . (1)
This is a volume conserving strain which has the nice property that E(-x) = E(x) for an hcp lattice. Therefore the energy/strain relationship is
E(x) = E0 + ½ V0 C44 x2 + O[x4] (2)
The problem with this strain, just as in the C11-C12 case, is that the symmetry here is so low that the atoms can move rather freely through the unit cell. In this case the strained hcp lattice then has the form
| a1 | = ( | ½ a , | - ½ 3½ a , | - ¼ 3½ x a ) | |
| a2 | = ( | ½ a , | ½ 3½ a , | ¼ 3½ x a ) | . (3) |
| a3 | = ( | 0 , | ½ x c , | ( 1 + ¼ x2 ) c ) |
The symmetry turns out to be C2/m (#12 in the International Crystallography tables), a centered monoclinic lattice with the atoms sitting on the 4m sites. Unfortunately, the 4m sites are listed as ±(x,0,z), i.e., there are two internal parameters needed to describe the lattice. The basis vectors can be written in the form
| B1 | = | (1/3 - u) a1 + (2/3 + u) a2 + (1/4 + v) a3 | |
| B2 | = | (2/3 + u) a1 + (1/3 - u) a2 + (3/4 - v) a3 | , (4) |
The usual procedure to find C44 would be to pick a value x, find the values umin(x) and vmin(x) which minimize E(x,u,v), and fit E(x,umin(x),vmin(x)) to (2). However, at the moment I don't have a quick (i.e., script file type) minimization package available. What I'll do here is just calculate E(x,u=0,v=0). Since this is always bigger than the true E(x), except at x=0, we'll be calculating an upper bound on C44. I've saved the calculation of the fully relaxed elastic constant for another page.
To pull off this calculation we need the space group file for C2/m, which I've put in work/c44/spcgp1.12 .
We also need the k-point mesh file, which I've generated in the same way as in the equation of state (EOS) example. This file is stored in work/c44/kmesh.12 .
Finally, we need an input file, which I've place in work/c44/SKIN . Since we're taking u=v=0, it's rather easy to construct. The only trick is to remember we're using strain 6, and that E(-x)=E(x).
Now it is simple to run the code. We get the following work/c44/SKENG file:
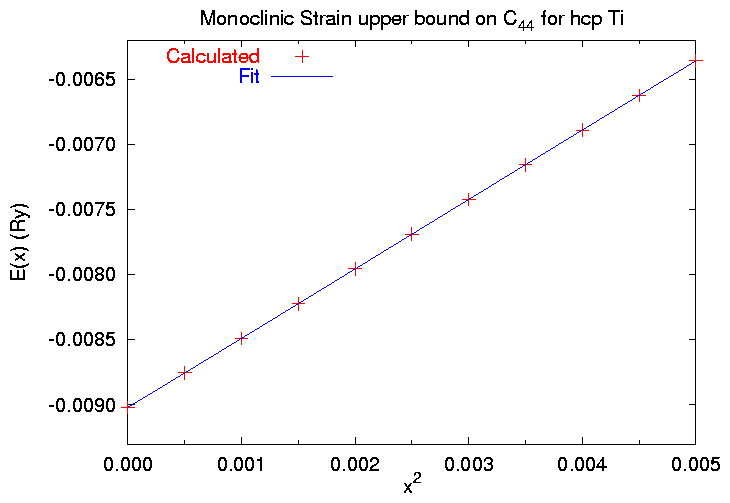
Note that we're plotting and fitting E(x) versus x2.
Then the gnuplot
script work/c44/c44fit.gnu
gives the information
and the plot:
So in this section we've shown that
C44 < 70.3 GPa .
Look at the fully relaxed calculation of
C44 in an hcp
lattice.
Go back to the Example X home page.
Look at other examples.
Get other parameters from the Tight-binding periodic
table. Return to the static Reference
Manual.
x^2= 0.0000 220.088000 .128472502 -.009018141
x^2= 0.0005 220.088000 .128276347 -.008754376
x^2= 0.0010 220.088000 .128082626 -.008489157
x^2= 0.0015 220.088000 .127891253 -.008223074
x^2= 0.0020 220.088000 .127701997 -.007956451
x^2= 0.0025 220.088000 .127514752 -.007689725
x^2= 0.0030 220.088000 .127329117 -.007423022
x^2= 0.0035 220.088000 .127144952 -.007156567
x^2= 0.0040 220.088000 .126962066 -.006890480
x^2= 0.0045 220.088000 .126780310 -.006624841
x^2= 0.0050 220.088000 .126599575 -.006359702
$ gnuplot c44fit.gnu
Using eo = -0.009018141 vo = 220.088
Edit c44fit.gnu to change
Press enter to continue
Fit info deleted. See work/c44/fit.log for details
C_{44} < 70.3023705195851 GPa
Press enter to quit
$