Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example XII

Finding the Electronic Density of States and Band Structure for Monatomic Cubic Crystals

Electronic structure calculations such as our tight-binding method determine the energy eigenvalues en at some point k in the first Brillouin zone. If we know the eigenvalues at all points k, then the band structure energy (the total energy in our tight-binding method) is just

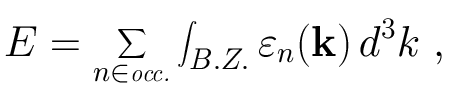
Integral of eigenvalues over the Brillouin zone
where the integral is over the occupied states of below the Fermi level.

Alternatively, we might want to know the density of eigenvalues in the energy range [e,e+de], where de is small enough so that this density doesn't change much over this interval. This is known as the electronic density of states (DOS). It is obviously useful, since it tells you the energy states electrons can occupy in the crystal. In an insulator density of states actually vanishes at the Fermi level, meaning that electrons cannot move through the crystal without the application of a lot of energy.

If we know the band structure at every point in the Brillouin zone, then the DOS is given by the formula

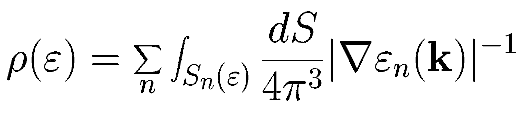
Integral formula for the DOS
where Sn(e) is the surface in k space at which the nth eigenvalue has the value e.

Obviously we can not evaluate this integral directly, since we don't know en(k) at all points, and can only guess at the properties of its gradient. One common approximation is to use the tetrahedron method, which divides the Brillouin zone into (surprise) tetrahedra, and then linearly interpolates within the tetrahedra to determine the gradient. This method is an approximation, but its accuracy obviously improves as we increase the number of k-points.

To begin this example, you will need the qlmtconvert.f and the dostet.f source files. The qlmtconvert converts the QLMT file created by the static program into a format that is usable by dostet. The dostet program will compute the Density of States (DOS) for the s, p, and d orbitals, along with the total DOS.

The dostet program takes as its input the dosdat.in file. The dosdat.in file is formatted as follows:

  1. The name of the element (e.g. "Ag", or "W", or "Re", etc.).
  2. The number of valence electrons and atomic weight of the element.
  3. The lattice constant in Bohrs.
  4. The type of k-point mesh to be used ( 2 or 4 for SC; 4 or 8 for BCC and FCC ), the number of bands to be computed, and the number of columns in the *.eng file (ALWAYS 6 in these examples).
    • For SC, 2 → 35 k-points, 4 → 165 k-points
    • For BCC, 4 → 55 k-points, 8 → 285 k-points
    • For FCC, 4 → 89 k-points, 8 → 505 k-points
    • The columns in the *.eng file correspond to the components of the Density-of-States: eigenvalue, s-state, p-state, d-state, 0, 0
  5. The minimum, step size, and maximum range of the DOS to be plotted.

An fcc crystal -- Silver

For our first example we will look at the electronic DOS and bandstructure of silver, a classic simple cubic material.

Create a directory fcc with the following files: 

$ ls -al fcc/
total 108
-r--r--r-- 1 ssayed2 users  7130 Aug 17 13:42 ag_par
-r--r--r-- 1 ssayed2 users  971  Aug 17 13:32 bandplot.in
-rw-r--r-- 1 ssayed2 users   206 Aug 17 13:45 dosdat.in
-rwxr-xr-x 1 ssayed2 users  3050 Aug 17 13:47 dosplot.ag.fcc.gnu
-rw-r--r-- 1 ssayed2 users 25767 Aug 17 13:43 kpoints.fcc505
-rw-r--r-- 1 ssayed2 users  4195 Aug 17 13:43 kpoints.fcc89
-rw-r--r-- 1 ssayed2 users  1386 Aug 17 13:46 SKIN.band
-rw-r--r-- 1 ssayed2 users   963 Aug 17 13:46 SKIN.dos
-rw-r--r-- 1 ssayed2 users 10003 Aug 17 13:42 spcgrp.fcc

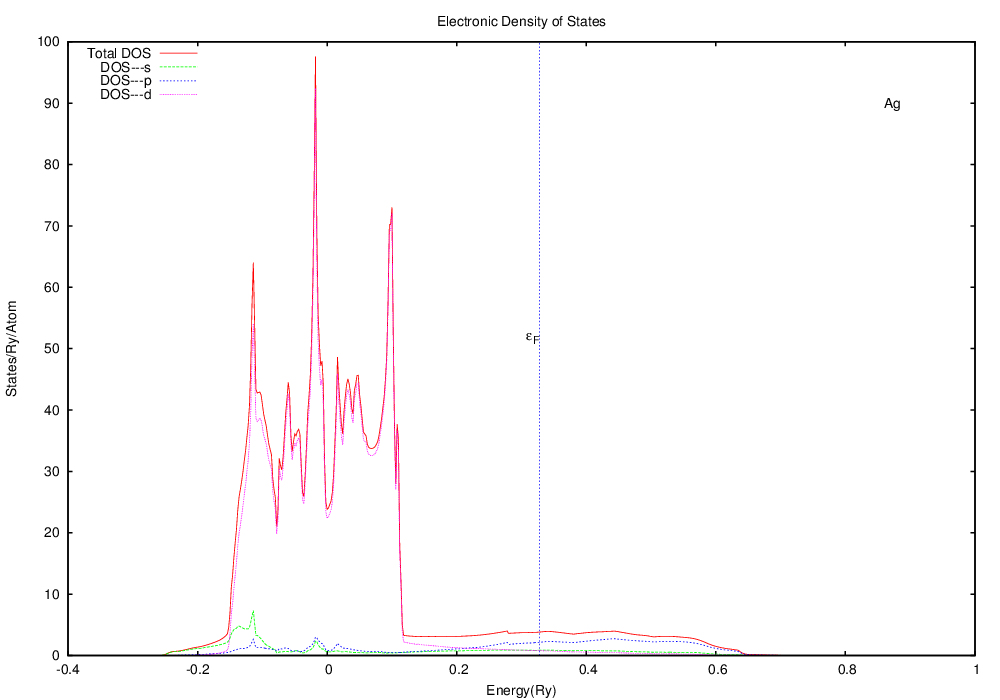
Density of States for TB fcc Silver

To create your own plots, I have provided a template gnuplot script that you can modify for your own purposes. At a minimum, you will need to find-replace the string "Elem" with the element symbol that you are working with (e.g. "Ag", "W", "Re", etc. ). You will also need to find-replace the string fermi with the calculated value of the Fermi energy. You can find the calculated value of the Fermi energy in the output file dosapw.itp, where it is listed as the first value in the file.


Now let's compute the bandstructure of Silver. For this, you will need the bandplot.f source, and bandplot.in.


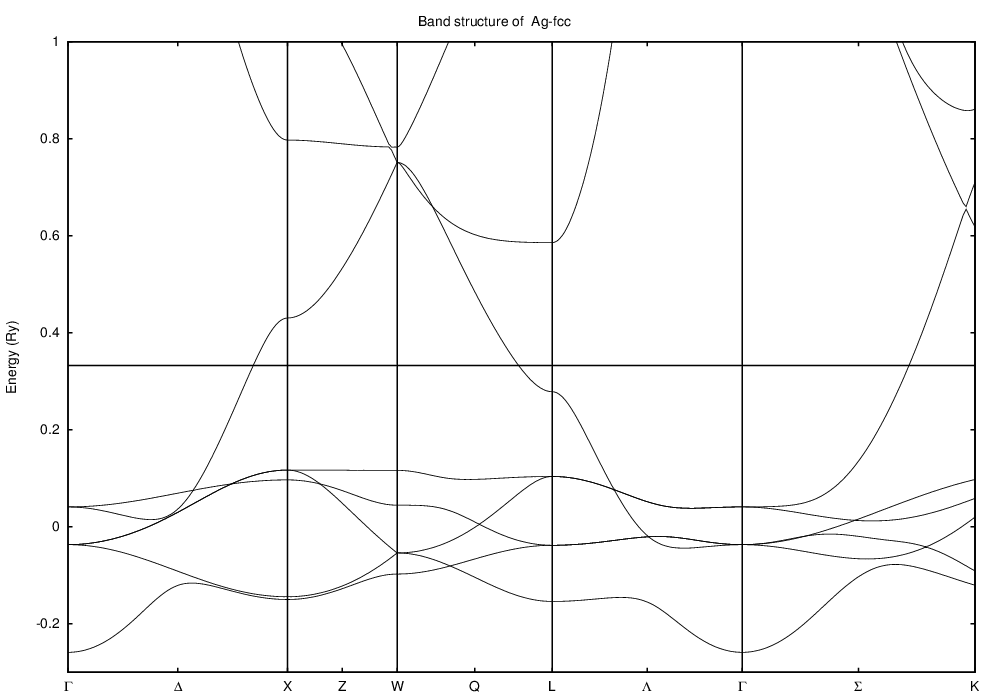
Band Structure for TB fcc Silver

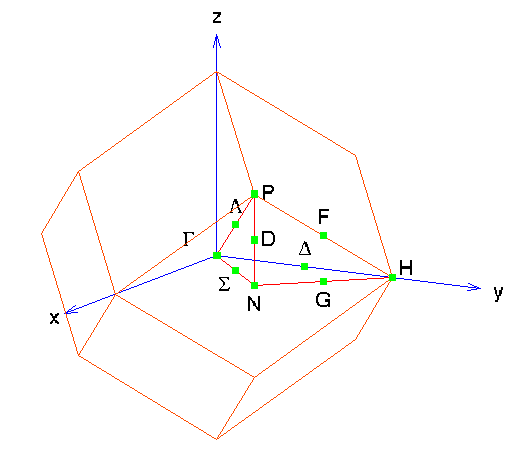
This last picture represents the band structure along certain high-symmetry lines in the Brillouin zone of the fcc lattice:

High Symmetry Points in the fcc Brillouin zone

A bcc crystal -- Tungsten

That was relatively straight-forward. Now we want to do something similar for tungsten. This is a body-centered cubic metal with an equilibrium lattice constant of 3.16 Å. Get the parameter file w_par from the Tight-Binding Parameters page. I recommend doing this calculation in a new directory.

Create a directory bcc with the following files: 

$ ls -al bcc/
total 208
-rw-r--r-- 1 ssayed2 users   1147 Aug 19 13:40 bandplot.in
-rw-r--r-- 1 ssayed2 users    189 Aug 17 13:48 dosdat.in
-rwxr-xr-x 1 ssayed2 users   3049 Aug 17 13:48 dosplot.w.bcc.gnu
-rw-r--r-- 1 ssayed2 users  13996 Aug 17 13:47 kpts.bcc285
-rw-r--r-- 1 ssayed2 users   2541 Aug 17 13:47 kpts.bcc55
-rw-r--r-- 1 ssayed2 users   1391 Aug 17 13:49 SKIN.band
-rw-r--r-- 1 ssayed2 users    962 Aug 17 13:49 SKIN.dos
-rw-r--r-- 1 ssayed2 users  10003 Aug 17 13:48 spcgrp.bcc
-r--r--r-- 1 ssayed2 users   7131 Aug 17 13:47 w_par

The DOS should look something like this:

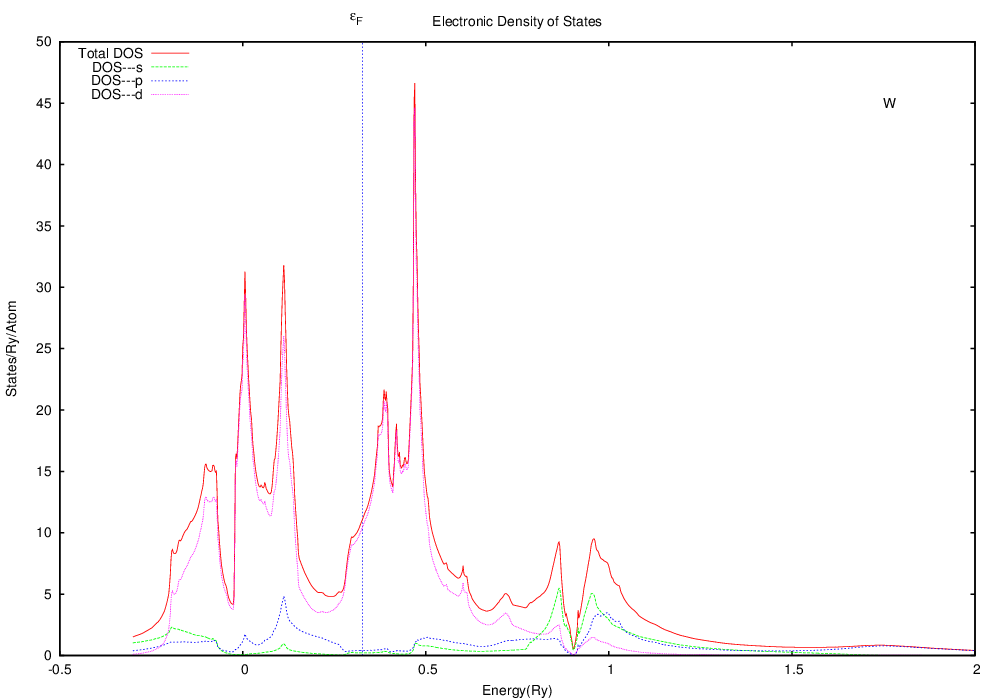
TB DOS of bcc Tungsten

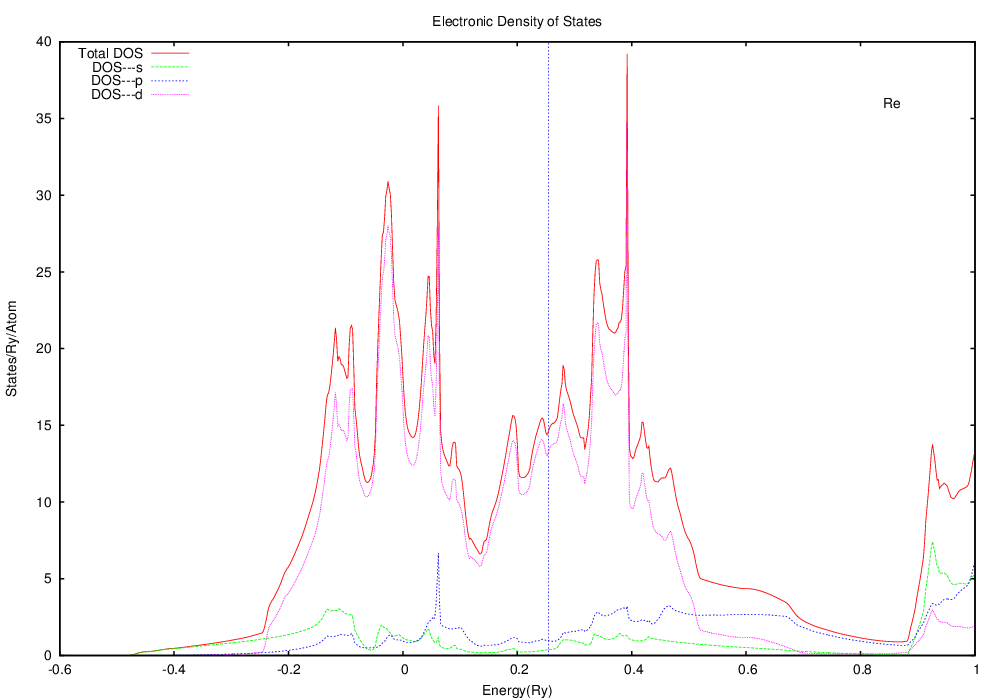
Note that this is substantially different from silver. The Fermi level (the highest state occupied by electrons) is well within the d bands, in contrast to silver, where the Fermi level was in a region with little contribution from the d states. If you think that this may have something to do with silver being a ductile fcc crystal and tungsten being a somewhat brittle bcc crystal, you're right.

Now let's compute the bandstructure of Tungsten. For this, you will need the bandplot.f source, and bandplot.in.

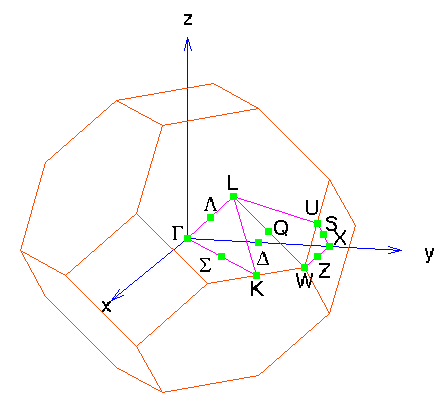
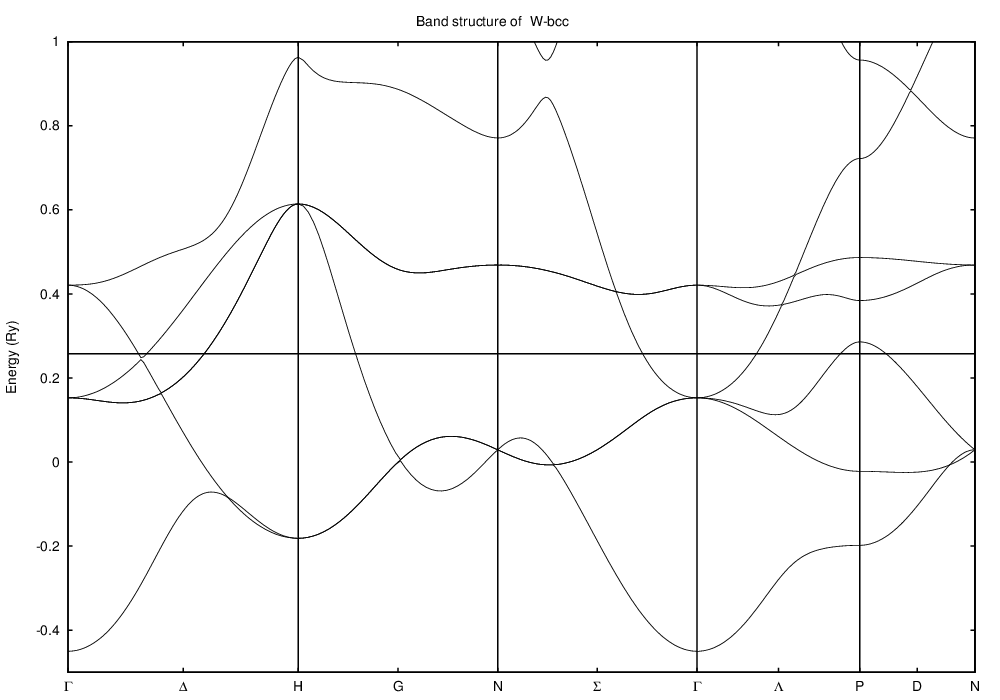
The band structure for bcc materials is ploted along these high-symmetry directions:

High Symmetry Points in the bcc Brillouin zone

and looks like this for tungsten:
TB bandstructure of bcc Tungsten

A hypothetical simple cubic crystal -- Rhenium

The only element which has a simple cubic ground state is Polonium, something we have not parameterized. So I'll take a hypothetical simple cubic structure of, say, Rhenium, with parameters re_par, and look at its DOS and band structure in a simple cubic lattice. To get a lattice constant, note that in its equilibrium hexagonal close-packed structure each Rhenium atom occupies 14.7 Å3. This corresponds to a simple cubic lattice constant of 2.45 Å. Since a simple cubic structure is usually less dense than a close packed structure, let's do the calculation at 2.60 Å.

For this example, I'll leave it to you to run the right program, and I will just show the results. The necessary files are listed below:

Create a directory sc with the following files: 

$ ls -al sc/
total 160
-rw-r--r-- 1 ssayed2 users  1144 Aug 24 16:17 bandplot.in
-rw-r--r-- 1 ssayed2 users   189 Aug 24 16:17 dosdat.in
-rwxr-xr-x 1 ssayed2 users  3081 Aug 24 16:17 dosplot.re.sc.gnu
-rw-r--r-- 1 ssayed2 users  9247 Aug 24 16:18 kpts.sc165
-r--r--r-- 1 ssayed2 users  7131 Aug 24 16:18 re_par
-rw-r--r-- 1 ssayed2 users  1384 Aug 24 16:18 SKIN.band
-rw-r--r-- 1 ssayed2 users   957 Aug 24 16:18 SKIN.dos
-rw-r--r-- 1 ssayed2 users 10003 Aug 24 16:18 spcgrp.sc

The DOS looks like this:

TB DOS of simple cubic Rhenium

This is a diagram showing the high-symmetry directions of the simple cubic Brillouin zone:

High Symmetry Points in the simple cubic Brillouin zone

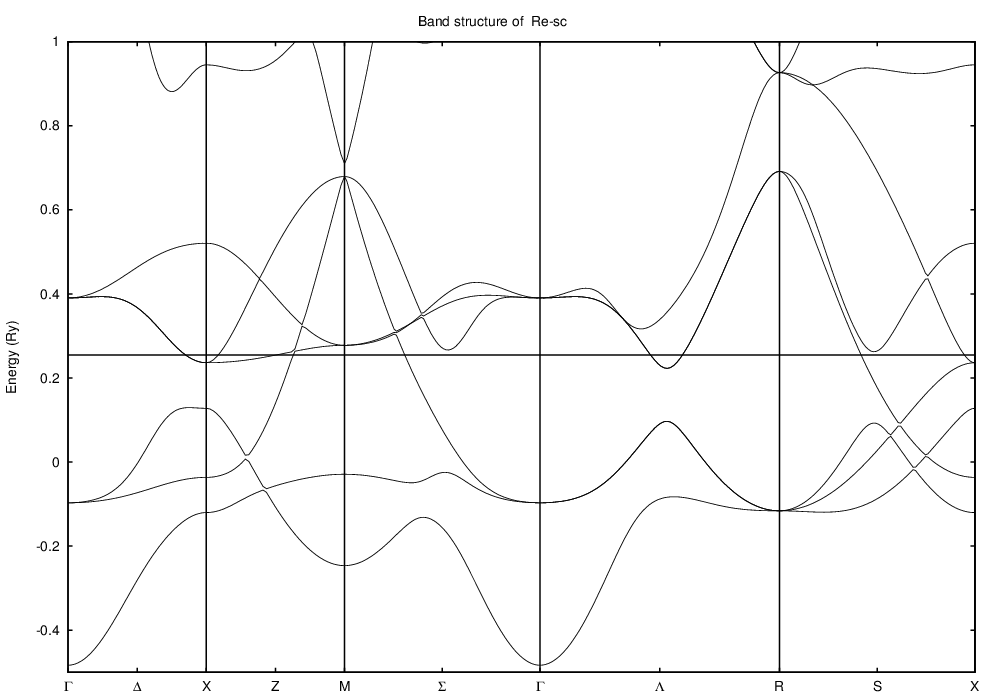
and here is the band structure along those points:

TB bandstructure of simple cubic Rhenium

Now you can do this for all the other elements.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

static Home Page   Introduction   About Version 1.11   Installation   List of Files   Usage   Input Files   Output Files   Trouble Shooting   Appendix

Return to the static Reference Manual.

The appearance of external hyperlinks does not constitute endorsement by the United States Department of Defense, the United States Department of the Navy, and the Naval Research Laboratory of the linked web sites, or the information, products or services contained therein. For other than authorized activities such as military exchanges and Morale, Welfare, and Recreation (MWR) sites, the United States Department of Defense, the Department of the Navy, and the Naval Research Laboratory does not exercise any editorial control over the information you may find at these locations. Such links are provided consistent with the stated purpose of this DoD web site.

Return to CCMS home page