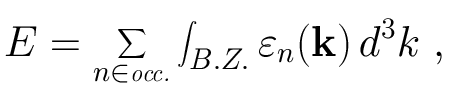
Both first-principles and tight-binding electronic structure total energy calculations require integrals of wavefunctions and/or eigenvalues over the Brillouin zone. Thus, in the NRL tight-binding formalism the total energy of a crystal is given by
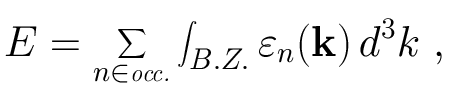
where the sum is over the occupied states of the system at the wave vector k in the first Brillouin zone. In practice the integral must be approximated by a sum over selected k-points in the Brillouin zone:
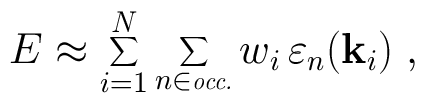
The links below take you to predefined k-point meshes for several common lattices. We list both regular and special k-point meshes, and take the symmetry of the lattice into account to minimize the computational work. Each set of k-points is also cross referenced to the appropriate entries in the Crystal Lattice Structures database.
The k-point database
| Cubic Systems | Other Systems |
|---|---|
| face-centered cubic lattices | Hexagonal Lattices |
| body-centered cubic lattices | |
| simple cubic lattices |
The Center for Computational Materials Science (Code 6390) maintains a Preprint & Reprint Library of its publications.
Return to the Code 6630 Home Page.
