Pre-defined k-point sets for Crystalline calculations: hexagonal lattices

REGULAR
Order ( 3, 3) (28 points)	Order (12, 6) (427 points)
Order ( 6, 3) (76 points)	Order ( 9, 9) (370 points)
Order ( 6, 6) (133 points)	Order (12, 9) (610 points)
Order ( 9, 6) (259 points)	Order (12,12) (793 points)

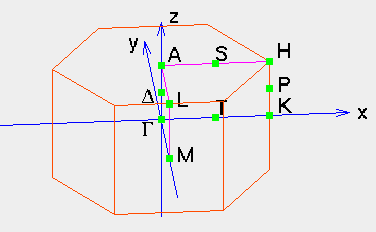
*The First Brillouin zone of a hexagonal lattice, with high symmetry k points marked.*

The above k-point meshes were generated for hexagonal lattices, where the crystal has full hexagonal symmetry, and the primitive lattice vectors are given by

a₁ = ( ½ a , -½ 3^1/2 a , 0 )
a₂ = ( ½ a , +½ 3^1/2 a , 0 )
a₃ = ( 0 , 0 , c )

with reciprocal lattice vectors

b₁ = ( 2 pi/a , - 2 pi 3^-1/2/a , 0 )
b₂ = ( 2 pi/a , + 2 pi 3^-1/2/a , 0 )
b₃ = ( 0 , 0 , 2 pi/c ) (one hopes that some future version of HTML will be able to print pi = 3.1415926... in the original Greek)

these lattices include the space groups

P6/mmm (#191) (Al₂B (ideal omega))
P6₃mmc (#194) (hcp, graphite, hexagonal Laves, D0₁₉)

For hexagonal lattices we only list "regular" k-point meshes, and only those meshes which include the high symmetry Gamma, A, M, K, L, and H points in the first Brillouin zone. Points are listed in lattice-coordinate format. The order of the mesh is given by a pair of numbers. The first is the number of k-points which lie on the line between the origin and the point M (2 pi/a, 0, 0) in reciprocal space, or at M. The second is the number of points between the origin and (or at) the point A (0, 0, pi/c).

Return to the k-point page