Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example IX

Constructing the Density of States (DOS)

On the previous page we used static to produce a QLMT file to be used to construct a Density of States for hcp Ruthenium. This page shows how to convert this particular QLMT file into an approximate electronic density of states.

There are accurate ways to construct the DOS, most notably the tetrahedron method, and then there is my way. My way uses the program qdos.f, which produces a ``quick and dirty'' DOS using the implicit formula for the DOS defined by our method of doing eigenvalue-energy sums. A somewhat more detailed explanation of this is contained in the comments within the source code.

Compile qdos.f and place the executable somewhere in your path. Then go to your working directory and run the code.

$ ./qdos 0.005 -0.389 0.500 0.0002 < QLMT > dos_0.0050

Let's take a quick look at the output file dos_0.0050. The first few lines look like this:

     -.38900      .00067      .10740  1.3784E+01     -.00026
     -.38880      .00069      .11017  1.3964E+01     -.00026
     -.38860      .00072      .11298  1.4140E+01     -.00027
     -.38840      .00074      .11583  1.4309E+01     -.00028
     -.38820      .00076      .11871  1.4473E+01     -.00029
     -.38800      .00079      .12162  1.4631E+01     -.00030
     -.38780      .00081      .12456  1.4783E+01     -.00031
     -.38760      .00084      .12753  1.4928E+01     -.00032
     -.38740      .00086      .13053  1.5067E+01     -.00033
     -.38720      .00089      .13355  1.5199E+01     -.00034

On each line,

Column 1 contains the current energy.
Column 2 contains the integrated DOS up to that energy. That is, this is the total number of electronic states with energy below the current energy. On the first line this number is not zero because of the temperature broadening we are using. Essentially we are spreading each state out over about 5mRy of energy, so a substantial part of the lowest energy state (-0.389Ry) is below our window.
- We can use this result to locate the Fermi level. Ruthenium has eight electrons per atom, or 16 electrons in the hcp unit cell. Doing a search for "16." in dos_0.0050 yields:
```
      .24000    15.99180    22.10841  1.6709E+02     -.01290
      .24020    15.99623    22.14216  1.7045E+02     -.01183
      .24040    16.00066    22.17657  1.7354E+02     -.01077
      .24060    16.00510    22.21156  1.7636E+02     -.00970
```
  so the Fermi level is between 0.24020 and 0.24040. This is in agreement with the results of the SKENG file:
```
 experiment           183.661901     .240370332    -.010923624
```
Column 3 contains the actual DOS. The units here are electronic states/energy unit (Ry)/unit cell.
Column 4 has the energy derivative of the DOS.
Column 5 contains the integrated density up to the current density. From the above example, a crystal with 15.99180 electrons per unit cell would have a Fermi level of 0.24000 Ry and an energy of -0.01290 Ry. A corollary is that the energy at the Fermi level should be consistent with the energy in the SKENG file, and we see that it is.

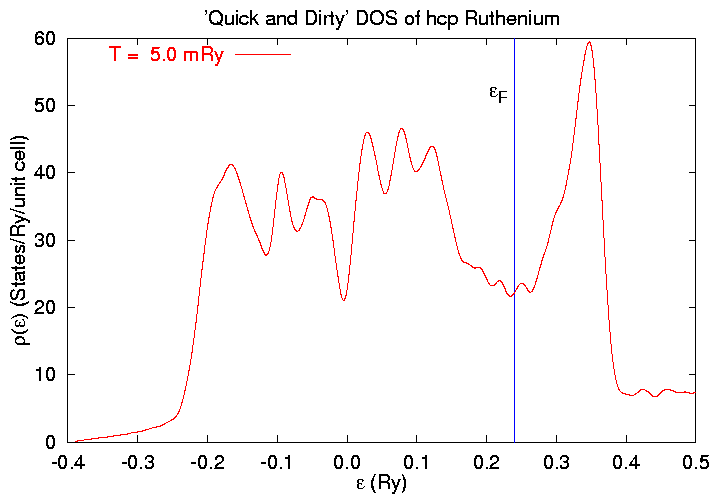
We can now plot out the DOS for Ruthenium using a gnuplot script:

We can compare this result with the First-principles calculation from NRL's Electronic Structures Database:

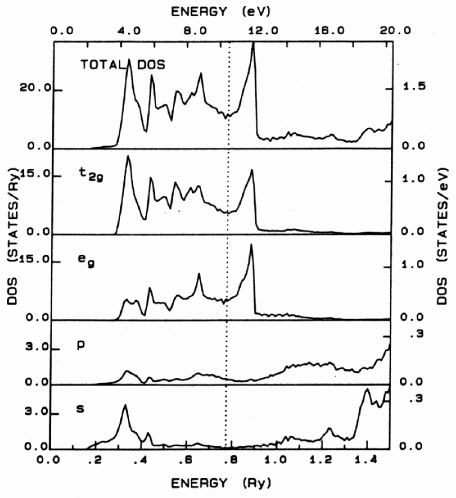
Aside from the arbitrary shift in energy, these curves are in pretty close agreement.

Temperature Dependence of the DOS

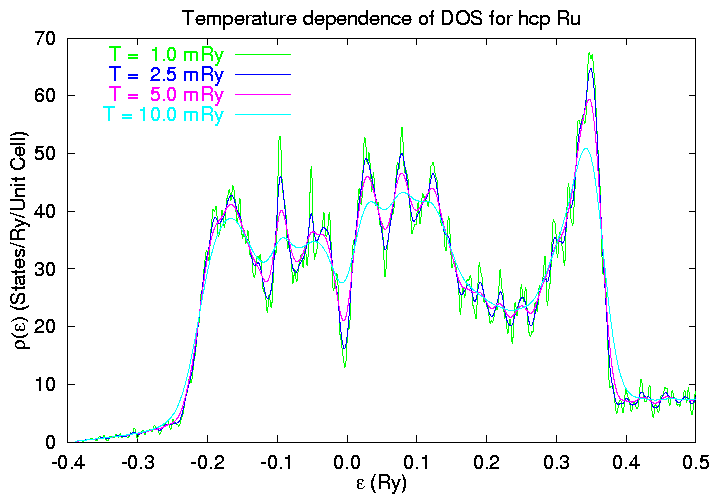
We'll now consider the behavior of the DOS as a function of the Fermi temperature used in Gillan's method. We can guess that if the temperature is too small the DOS plot will degenerate into a series of spikes, and we'll have to have a very fine grid to see them at all. On the other hand, when the temperature is too large everything gets smeared out.

The following script calculates the DOS at every temperature on its command line, assuming the temperatures are in Rydbergs:

#!/bin/sh
for temp
do
./qdos $temp -0.389 0.5001 0.0005 < QLMT > dos_$temp
done

We'll run this for a few representative temperatures:

tscript 0.0010 0.0025 0.0100

and plot them and our original data using this script:

Our predictions are correct, but over the rather broad range 1 mRy<T<10 mRy this ``Quick and Dirty'' DOS remains fairly consistent.

Now back to the DOS setup page.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

static Home Page Introduction About Version 1.11 Installation List of Files Usage Input Files Output Files Trouble Shooting Appendix

Return to the static Reference Manual.