Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example VIII

This is in a way a continuation of example 7, as we use static to make a band structure plot of bcc Tantalum. We'll continue looking at electronic structures in example 9, where we'll plot the electronic density of states (DOS). If you haven't studied it already, you might want to go back and look at example 7 before continuing here, as I'm going to go through some of this rather rapidly.

In the ground state tantalum forms a bcc lattice, so its Brillouin zone is the same as the Wigner-Seitz cell of an fcc lattice. We'll plot the band structure along several lines connecting the high symmetry points of the Brillouin zone, as show in the figure below.

Surprisingly, the tight-binding parameters for tantalum can be obtained from the tight-binding periodic table under ``Ta'', so find them and save them in your working directory as ta_par.

The space group file for the bcc lattice was downloaded in example 1, so we'll steal spcgrp.bcc from there and rename it spcgrp.

As before, we'll defer the discussion of the k-point ``mesh'' for a few moments.

The main part of the SKIN file is in the standard form. The only differences from example 7 are cause by the fact that this is a bcc lattice of Tantalum, and that Tantalum's equilibrium lattice constant is 3.30 Å = 6.236 Bohr:

Mode=9               Stripped QLMT file
0.002  0.500         (T_{Fermi}, Eigenvalue cutoff for P calculation)
ta_par
BCC Tantalum -- Band Structure
 bcc equilibrium     (20 character label for SKENG)
 0.00                (Electrons in addition to nominal Ta charge (=5/atom))
 2                   (bcc lattice, read in cubic lattice constant a)
 6.236               (lattice constant in Bohr)
 0                   (No additional strains applied)
 1                   (Atoms in the unit cell)
 4 4 4               (Neighbor search cutoff indices)
F                    (Logical variable -- no internal displacements)
 1  0.000  0.000  0.000  0 0 0   (Position of atom in Lattice coordinates)
NEWSYM=T             (Generate new set of k-points)
LATTIC=1             (Lattice type / Next is spacegroup file name:)
spcgrp
ILAT=F               (Space group file in Cartesian Coordinates)

Note that we changed from Mode=6 to Mode=9. This eliminates the angular momentum decomposition of the eigenstates, saving some time and, in the case of a large lattice, a lot of space.

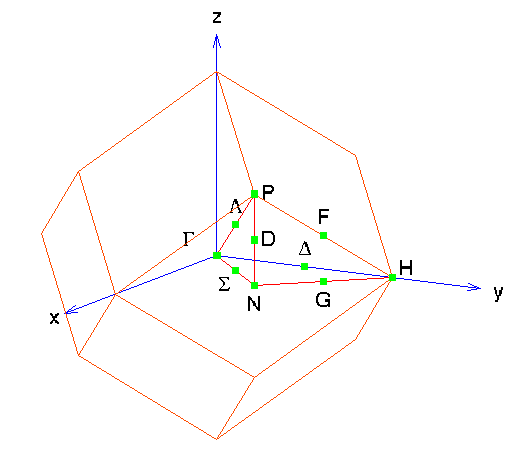
As in example 7 The k-point generation routine looks at lines through the Brillouin zone rather than over the entire space. As you can see from the figure, we have a different set of lines and high-symmetry points here, since the shape of the Brillouin zone has changed.

The lattice types table tells us that the ``standard'' primitive lattice vectors of the bcc lattice are

• a₁ = ( -½ a , ½ a , ½ a)    
• a₂ = ( ½ a , -½ a , ½ a)    
• a₃ = ( ½ a , ½ a , -½ a)   .

This means that the primitive vectors of the reciprocal lattice are specified by

• a₁ = 2 Pi ( 0 , 1/a , 1/a)    
• a₂ = 2 Pi ( 1/a , 0 , 1/a)    
• a₃ = 2 Pi ( 1/a , 1/a , 0)
  .

So now we want to generate the k-points along the lines

1. Gamma --> H via Delta
2. X --> P via F
3. P --> Gamma via Lambda
4. Gamma --> N via Sigma
5. N --> P, via D, and then back to N via D'
6. D' --> H', vi G   .

As before, we'll use the "999" option to the k-point generating routine kptin.f. This leads to the following SKIN file fragment:

  999
    6
41  0.00  0.00  0.00    0.50 -0.50  0.50    (Gamma -> Delta -> H)
41  0.50 -0.50  0.50    0.25  0.25  0.25    (H->F->P)
41  0.25  0.25  0.25    0.00  0.00  0.00    (P->Lambda->Gamma)
41  0.00  0.00  0.00    0.00  0.00  0.50    (Gamma->Sigma->N)
41  0.00  0.00  0.50    0.25  0.25  0.25    (N->D->P)
41  0.25  0.25  0.25    0.50  0.50  0.00    (P->D'->N')
41  0.50  0.50  0.00    0.50  0.50  0.50    (N'->G'->H')

Now the program is ready to run.

Now go to the output discussion to see what will happen, and to view the band structure plot.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

Return to the static Reference Manual.