Last Modified 29 May 1998

The ``Static'' Tight-Binding Program: Example V -- Output

If you've followed the steps on the setup page, your working directory should now look something like this:

$ ls -l
total 56
-rw-r--r--   2 mehl     usr         6960 May 29 13:31 SKIN
-r--r--r--   2 mehl     usr         7221 May 29 13:01 bccc44.08
-r--r--r--   2 mehl     usr         7200 May 29 13:01 nb_par
-rw-r--r--   2 mehl     usr         1559 May 29 13:31 spcgrp

Now run the static code in this directory. You'll get something like this:

$ static > output
$ ls -l
-rw-r--r--   1 mehl     bind         630 May 29 13:51 SKENG
-rw-r--r--   2 mehl     usr         6960 May 29 13:31 SKIN
-rw-r--r--   1 mehl     bind       32574 May 29 13:51 SKOUT
-r--r--r--   2 mehl     usr         7221 May 29 13:01 bccc44.08
-r--r--r--   2 mehl     usr         7200 May 29 13:01 nb_par
-rw-r--r--   1 mehl     bind       24178 May 29 13:51 output
-rw-r--r--   2 mehl     usr         1559 May 29 13:31 spcgrp

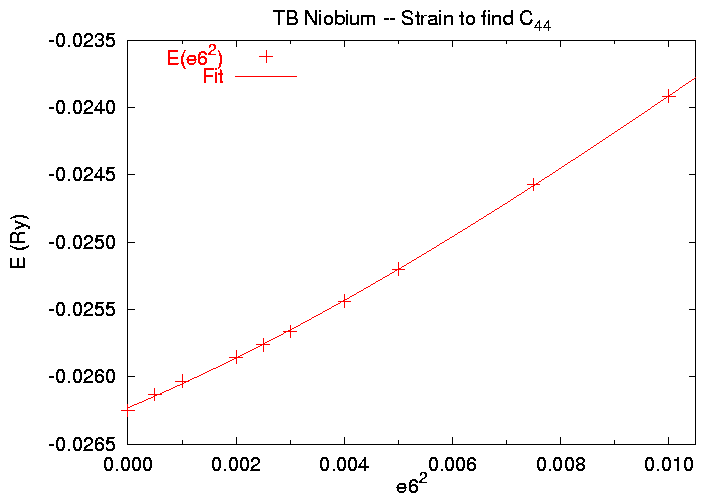
As usual, we are most interested in the SKENG file:

 e6^2= 0.0000         121.251836     .130621233    -.026252012
 e6^2= 0.0005         121.251836     .130748653    -.026130711
 e6^2= 0.0010         121.251836     .130772820    -.026033556
 e6^2= 0.0020         121.251836     .130640009    -.025855516
 e6^2= 0.0025         121.251836     .130538390    -.025763392
 e6^2= 0.0030         121.251836     .130443331    -.025663667
 e6^2= 0.0040         121.251836     .130374474    -.025439639
 e6^2= 0.0050         121.251836     .130417789    -.025200571
 e6^2= 0.0075         121.251836     .130847311    -.024573468
 e6^2= 0.0100         121.251836     .131691173    -.023917255

The energy increases monotonically with strain, supporting our notion that the bcc phase is the the ground state. Now remember that Equation 2 tells us that the energy E should be close to a linear function of the squared strain e₆². We'll therefore write a gnuplot script, nbfit.gnu, which fits this data to the functional form:

E(E₀,C₄₄,a,b,e₆²) = E₀ + ½ V [ C₄₄ e₆² + a e₆⁴ + b e₆⁶] (3) .

Note that in (3) we know the volume V, and want to determine the remaining parameters E₀, C₄₄, a, and b to best fit the data in SKENG.

Now run the script (which will leave behind a file nbplot.gnu for posterity):

$ gnuplot nbfit.gnu
Current Volume is 121.251836  Correct if necessary
Press  to continue
[If the volume is not correct, edit cufit.gnu to fix it.]
[fitting information deleted.  See fit.log.]
Found C_{44} = 41.2367025059893 GPa at V = 121.251836 Bohr^3
Press  to conclude

The fit finds C₄₄ = 41 GPa. This should be compared to the experimental value of 29 GPa and the first-principles value of 25 &GPa. Our value is a again a little high.

Return to the setup page.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

static Home Page Introduction About Version 1.11 Installation List of Files Usage Input Files Output Files Trouble Shooting Appendix

Return to the static Reference Manual.