Last Modified 17 December 1999

The previous pages described the setup, execution, and results for the calculation of the stacking fault and anti-stacking fault energy in Gold, using our Tight-Binding Parametrization for gold. This page discusses the efficiency of the code parallelization.

The static code is written if Fortran 77 using MPI calls. For single processor jobs a set of fake MPI calls is provided. This allows the same code to be used on single and multiprocessor systems.

A tight-binding calculation involves:

• The choice of parameterization file
• The construction of the lattice (periodicity of the crystal)
• The placement of the basis vectors (atom positions)
• The construction off the k-point mesh
• Search for the neighboring atoms
• Construction of on-site energies for each atom. Note that the user may substitute other parametrization schemes for ours at this step.
• Evaluation of Slater-Koster integrals for each pair. Note that the user may substitute other parametrization schemes for ours at this step.
• The calculation of the total energy and band structure, which includes a sum over k-points. At each k-point we must:
  • Construct the final Hamiltonian and Overlap Matrix
  • Solve the resulting generalized eigenvalue problem
  • Store the eigenvalues and, if appropriate, the eigenvectors
• Output of results in human or machine-readable form.

The static runs the k-point loop, highlighted in green, in parallel. Thus the code will scale only when the number of k-points is significantly larger than the number of processors used. We will see an example of this below. In general this is not a problem, because the static code is usually used to determine the energetics and electronic structure of rather small systems (< 100 atoms) with a rather large number of k-points (>O[100]).

The static code has successfully run in parallel mode on the ASC SP2 and Origin. It has been compiled and run on other SGI machines, and in serial mode on Intel/Linux and AIX/RS6000 platforms. In its default configuration it uses no external libraries except those needed by the Fortran compiler and MPI. Therefore we are confident that this code can be readily ported to other machines. The success or failure of the parallelization on these machines will depend on the machine architecture.

For the target machines (SP2 and Origin at ASC), we ran the both test calculations (r24 and r48) using 1, 4, 8, and 16 processors. In all cases the output SKENG and SKOUT files were identical except for some discrepancies due to round-off. The timings on each machine were as follows:

Where the 16-processor times for the SGI are estimated because the machine will not print out "timex" results over 16 processors.

One of the CTP metrics was to measure the performance of the 16 processor system over the single processor system. This table gives the ratio of user time in the single processor system to time in the 16 processor system:

Note that the beta-test target ratio was 8 or greater. The results for the r24 run are worse than that for the r48 run because there are fewer k-points per processor in the smaller run. As noted before, the more k-points per processor the better the scalability of the code.

Another measure of parallelization is the amount of executed "core" code which is parallel, i.e. the ratio of parallel parts of the code to the total code. If we can ignore parallelization bottlenecks such as increased communication time with increasing numbers of processors, then the execution time of a code with n processors should go something like:

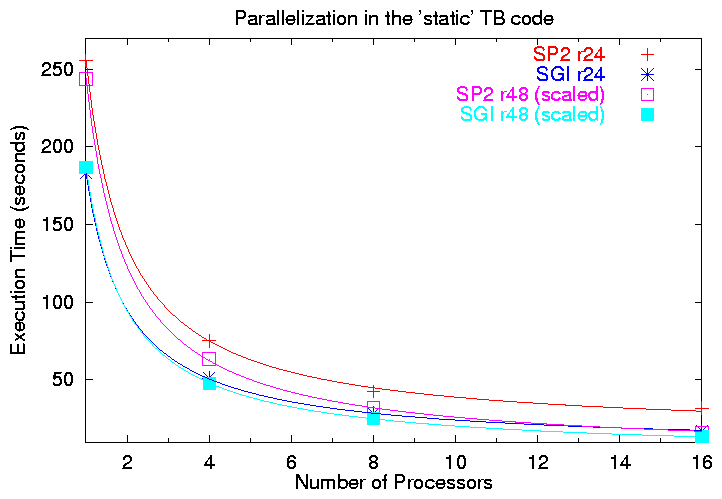
The graph below presents all of our timings and a fit to equation (1) for each machine and both problems. The only trick is that we have reduced the r48 results by a factor of 22.458. This factor comes about because the r48 calculation has 44 structures and 1202 k-points, versus 15 and 157, respectively, for the r24 calculation. All things being equal, then, the r48 calculation should take

The solid lines represent the fit to equation (1). By finding s and p for each machine and job we can also calculate the parallel efficiency (2):

The beta-test target for each machine was f > 80%.

This completes the discussion of the beta-test problem. Please feel free to look at other examples.

Previous: Looking at the results.

Get other parameters from the Tight-binding periodic table.

Return to the static Reference Manual.