Last Modified 17 December 1999
The static program is not limited to calculations involving infinite periodically repeating crystals. This example shows how we can use the program to determine the energy of a small cluster.
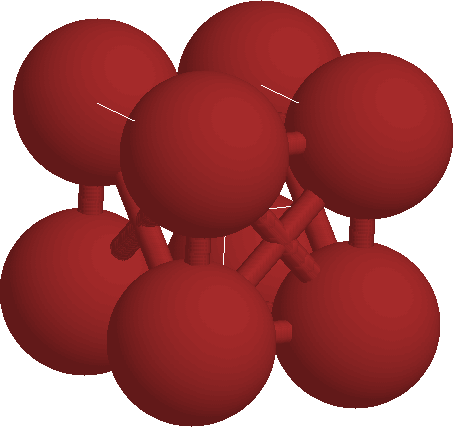
In particular, the cluster we have in mind is very simple, just eight carbon atoms arranged on the corners of a cube:
 |
We want to determine the equilibrium size of this cluster, i.e., the nearest neighbor spacing between the Copper atoms. |
Since the static code input requires us it include a set of primitive lattice vectors, it may not be obvious how to proceed. It turns out that the calculation is easy because of the short range of the tight-binding parameters, approximately 9 Angstroms or less. If we construct an incredibly huge unit cell, say a cube 1000 Bohr on a side, and keep the copper atoms near the origin, they will never interact with their periodic replicas. The only neighbors will be the atoms in the immediate cluster.
To start the code we grab a set of copper tight-binding parameters from the web, and save them in our working directory as cu_par.
Since the static code will still think that the calculation is in a periodic system, we need to give it a space group and a k-point mesh. The good news is that we don't have to think about this very hard, because there is no interaction between the unit cells. This means that the Bloch wavefunctions die before they reach any of the cluster replicas, so all k-points yield the same energy. Given that, we might as well take Gamma point as our k-point. (Unfortunately, the static code does not take advantage of the resulting reality of the Hamiltonian and overlap matrix.) We could write the k-point down in the file, or you can use the Gamma k-point file, which contains only one point.
Since we've picked our k-point, we don't need to worry about the space group, either. We can, and should, use the null space-group file, which has no symmetry except the identity (it's P1 and #1 in the Crystallographic Tables).
Saving all of these files in a working directory gives us
-r--r--r-- 2 mehl users 7130 May 28 1998 cu_par -r--r--r-- 43 mehl bind 28 Oct 28 1994 gamma.kpt -r--r--r-- 8 mehl bind 259 May 21 1998 spcgrp.P1
Now that we've got all of that, let's take a look at the SKIN file:
The start of the calculation is pretty predictable:
Mode=3 (Pressure is meaningless in a cluster calculation)
0.005 100.0 (T_{Fermi}, Eigenvalue cutoff for P calculation)
cu_par
The final results should not be particularly dependent on the choice of temperature, or the choice of Mode = 1 or Mode = 3. It turns out that there is a substantial gap between the highest occupied state and the lowest unoccupied state, so that this cluster is an insulator, at least when using our tight-binding parameters. (We leave the proof of this statment to the reader.)
Next we must decide on how to separate the unit cells. In many ways it doesn't matter too much, so we use a simple cubic unit cell with a separation of 100 Bohr between cells. Note that there is no interaction between copper atoms separated by more than 33 Bohr, twice the cutoff distance of 16.5 Bohr.
The experimental equlibrium distance between copper atoms in a crystal is 2.55 Angstroms = 4.80 Bohr. We'll allow for the possibility that the cluster might have a larger spacing and start our calculation at 5 Bohr, working down to find a minimum. The start of the SKIN file then looks like this:
Eight-atom copper cluster 5.000 (Label is interatomic distance) 0.00 (Electrons in addition to nominal Pd charge (=10/atom)) 4 (sc lattice, read in cubic lattice constant a) 100.0 (large lattice constant, infinitely separated cells) 0 (No additional strains applied) 8 (Atoms in the unit cell) 1 1 1 (Only because 0 0 0 leads to an error) F (Logical variable -- no internal displacements)
Note that we must specify a "1 1 1" search distance because "0 0 0" causes the program to crash in search2.f. In any case, there are only a limited number of neighbors subject to search.
So how do we construct the cube? A logical, symmetrical choice is to place the center of the cube at the origin and the cube axis along the Cartesian directions. There there are atoms at
( -r/2 r/2 r/2 ), ( r/2 -r/2 r/2 ), ( -r/2 -r/2 r/2), etc.
With the nearest neighbor distance set as r = 5 and a simple cubic unit cell size of 100.0 the atom would have a SKIN file entery like:
1 0.0025 0.0025 0.0025 0 0 0
That's fine for a lattice constant of 100, but what if we entered 225.3? To avoid difficulties, static provides an alternate entry method: If the atom type (the "1" here) is negative, then the atom type is set to its absolute value and the position of the atom is interpreted to be in Cartesian coordinates. Therefore our atomic positions become:
-1 2.500 2.500 2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 2.500 2.500 -2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 2.500 -2.500 2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 2.500 -2.500 -2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.500 2.500 2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.500 2.500 -2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.500 -2.500 2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.500 -2.500 -2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
Note that this trick is not confined to clusters. Even in a real periodic system a negative atom type tells the program that the atomic position is in Cartesian coordinates. Note that we can mix types, e.g., we could have written
-1 2.500 2.500 2.500 0 0 0 ('-1' -> positions in Cartesian coordinates)
1 0.025 0.025 -0.025 0 0 0 ('+1' -> positions in lattice coordinates)
though that would have been rather confusing.
Since we have an isolated cluster, the space group and k-point selection is particularly easy, as we mentioned above:
NEWSYM=T (Generate new set of k-points) LATTIC=1 (Lattice type / Next is spacegroup file name:) spcgrp.P1 ILAT=F (Space group file in Cartesian Coordinates) -1313 gamma.kpt
This ends the setup of the first structure. For succeeding structures we will make the interatomic distance smaller. For example, at a distance of 4.80 Bohr the entry to the SKIN file looks like this:
Eight-atom copper cluster
4.800 (Label is interatomic distance)
0.00 (Electrons in addition to nominal Pd charge (=10/atom))
4 (sc lattice, read in cubic lattice constant a)
100.0 (large lattice constant, infinitely separated cells)
0 (No additional strains applied)
8 (Atoms in the unit cell)
1 1 1 (Only because 0 0 0 leads to an error)
F (Logical variable -- no internal displacements)
-1 2.400 2.400 2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 2.400 2.400 -2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 2.400 -2.400 2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 2.400 -2.400 -2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.400 2.400 2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.400 2.400 -2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.400 -2.400 2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
-1 -2.400 -2.400 -2.400 0 0 0 ('-1' -> positions in Cartesian coordinates)
NEWSYM=F (Use old k-points)
where we keep the old k-point mesh.
I've written a complete SKIN file that you can use to run the program. The working directory now looks like this:
-rw-r--r-- 1 mehl bind 12220 May 21 17:42 SKIN -r--r--r-- 2 mehl users 7130 May 28 1998 cu_par -r--r--r-- 43 mehl bind 28 Oct 28 1994 gamma.kpt -r--r--r-- 8 mehl bind 259 May 21 1998 spcgrp.P1
After running the static code, the directory looks like this:
-rw-r--r-- 1 mehl bind 630 May 21 18:04 SKENG -rw-r--r-- 1 mehl bind 12220 May 21 17:42 SKIN -rw-r--r-- 1 mehl bind 34798 May 21 18:04 SKOUT -r--r--r-- 2 mehl users 7130 May 28 1998 cu_par -r--r--r-- 43 mehl bind 28 Oct 28 1994 gamma.kpt -rw-r--r-- 1 mehl bind 24075 May 21 18:04 output -r--r--r-- 8 mehl bind 259 May 21 1998 spcgrp.P1
where SKENG and SKOUT have their usual meaning
and output is the standard output. Note that the output file explicitly tells you that it is
converting atomic positions from Cartesian to lattice coordinates.
The SKENG file has some difficulty with the large volume
of our calculation:
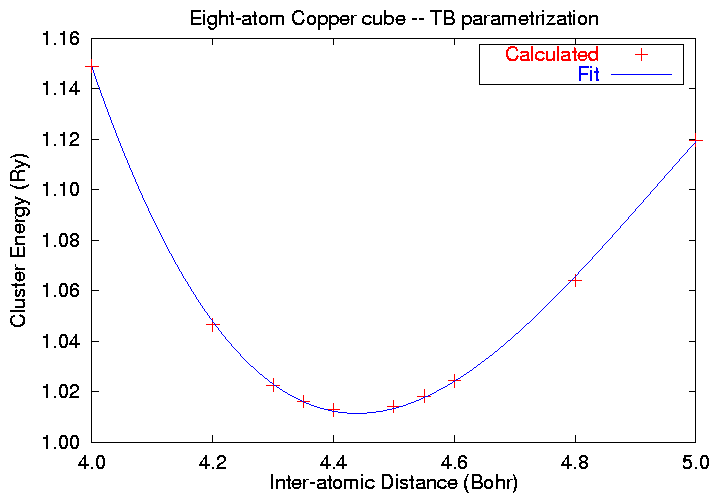
The minimum of this calculation is obviously around 4.4 Bohr. To
find the exact minimum, we fit the energies to a cubic polynomial in
the displacement by the use of this gnuplot
fitting script. This gives us the output:
Of course, it is unlikely that eight atoms of copper form a
simple cube, but you can investigate other structures using the
static code. For the widest possible search, however, you
will probably want to use the
Tight-Binding Molecular Dynamics (TBMD) code, also available
through the CHSSI program.
Look at other examples.
Get other parameters from the Tight-binding periodic
table. Return to the static Reference
Manual.
5.000 ************ .137678958 1.119595488
4.800 ************ .163069552 1.063931226
4.600 ************ .192971858 1.024286948
4.550 ************ .201186773 1.018186262
4.500 ************ .209707198 1.014046539
4.400 ************ .227690265 1.012693070
4.350 ************ .237169258 1.016060544
4.300 ************ .246987253 1.022553977
4.200 ************ .267697037 1.046367643
4.000 ************ .290909611 1.148887375
but this poses no problem because the volume of the unit cell (=
106 Bohr3) is irrelevant to our calculation.
Final set of parameters 68.3% confidence interval (one at a time)
======================= =========================================
eo = 1.01132 +/- 0.000328737 (0.0325056%)
ro = 4.43897 +/- 0.0019774 (0.0445463%)
a = 0.549211 +/- 0.00448344 (0.816343%)
b = -0.368962 +/- 0.0107137 (2.90374%)
which tells us that the minimum separation is 4.44 Bohr = 2.35
Angstroms, substantially smaller than the bulk separation. The
energy versus separation plot looks like this: