Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example X

Equation of State and equilibrium configuration of hcp Titanium

In this section we'll attempt to find the equilibrium configuration of hcp Titanium using our tight-binding parameters. I'm assuming you've followed the Example X home page and set up a working directory work, which should now look something like this:

drwxr-x---   2 mehl     users        1024 Jun  3 15:21 c11+c12/
drwxr-x---   2 mehl     users        1024 Jun  3 15:21 c11-c12/
drwxr-x---   2 mehl     users        1024 Jun  3 15:21 c33/
drwxr-x---   2 mehl     users        1024 Jun  3 15:21 c44/
drwxr-x---   2 mehl     users        1024 Jun  3 15:21 czz/
drwxr-x---   2 mehl     users        1024 Jun  3 15:21 eos/
drwxr-x---   2 mehl     users        1024 Jun  3 15:21 fixca/
-r--r--r--   1 mehl     users          39 Jun  3 15:20 kmesh
-r--r--r--   8 mehl     users        1511 May  7 15:40 spcgp1.hcp
-r--r--r--   3 mehl     users        7127 May  7 15:41 ti_par

Before we start calculating the EOS in earnest, we need to do a bit of preliminary work. We are going to be making a very large number of runs using the k-point meshes generated by the file kmesh. Since generation of k-points is slow, while reading k-points from a file is fast, we'll generate the k-point mesh here. This particular generation will only work for the P6₃/mmc (hcp) space group, but that will cover parts (i)-(v) of our tutorial. It will create a file called work/kmesh.194. You can see how it was created here.

Finding minimum energy c/a at fixed volume

In a cubic material, such as Palladium, finding the equation of state is easy: just enter a volume V_i, calculate E_i=E(V_i), repeat for awhile, and use a Birch (or another) fit on the set {V_i,E_i} to determine the equilibrium point and the EOS. In a hexagonal material it isn't quite that simple, because we have to find the minimum of the energy function E(V,c/a) at fixed volume. That is, for every volume V_i, we have to find the value (c/a)_i which minimizes the total energy of at that volume, and then construct E_i=E(V_i,(c/a)_i). Then we can fit the {V_i,E_i} pairs. Fortunately, in an hcp lattice, the atoms always remain at lattice coordinates (1/3,2/3,1/4) and (2/3,1/3,3/4), so we don't have to minimize the energy with respect to atomic positions.

There are many ways to perform the minimization. One of the easiest ways is based on a quasi-Newtonian method based on a script I call qnewt , which I've saved as work/eos/qnewt. This script takes a volume and a guess at the equilibrium c/a ratio for that volume as its input. It then gives you a better guess at the equilibrium c/a ration for that volume. You can use this guess in a new run of qnewt, and keep iterating until you get the equilibrium to the desired accuracy. Typically you can get the equilibrium energy to within 10^-5 Rydbergs in two or three steps.

To see how this works, let's pick an arbitrary volume, say 180 Bohr³, and run qnewt on that. We also need a guess at the equilibrium c/a ratio. The experimental value is 1.586, so we'll start with that.

$ qnewt 180 1.586
   1.57014000         180.000000     .153494107     .035772783
   1.58600000         180.000000     .153334993     .034924053
   1.60186000         180.000000     .153130047     .034338014
180.00000 1.62931217 0.033944498

The first three lines of output are the contents of an SKENG file, showing the energy as a function of c/a for three different values: 1.57014 (=0.99*1.586), our initial guess of 1.586, and 1.60186 (=1.10*1.586). Looking at the energies, we see that the minimum energy c/a ratio is probably going to be closer to 1.6 than 1.586. In fact, qnewt fits these three points to a parabola, and then finds that the minimum of this parabola is at 1.62931217, and the minimum value is 0.033944498. All of this information is printed out on the next line. It is unlikely that this is the correct minimum for our system, but it is a good next guess, so we'll try it again:

$ qnewt 180 1.62931217
   1.61301905         180.000000     .152952943     .034081198
   1.62931217         180.000000     .152641401     .033929475
   1.64560529         180.000000     .152271288     .034030406
180.00000 1.63094990 0.033928199

Now at least we've bounded the minimum, and the predicted minimum energy (0.033928199) is very near the minimum energy we've found so far (0.033929475). We could stop here, but one more iteration isn't a bad idea, just to make sure we're doing things correctly:

$ qnewt 180 1.63094990
   1.61464040         180.000000     .152924767     .034054374
   1.63094990         180.000000     .152606687     .033928436
   1.64725940         180.000000     .152230851     .034054143
180.00000 1.63095738 0.033928436

Now the predicted minimum energy and the minimum energy we've found are equal (0.033928436), so we are probably as close to the minimum as we can get. Now, if you look in your work/eos directory, you'll find a file named skeng.180, which contains all of the results of the SKENG files you've created for this volume:

   1.57014000         180.000000     .153494107     .035772783
   1.58600000         180.000000     .153334993     .034924053
   1.60186000         180.000000     .153130047     .034338014
   1.61301905         180.000000     .152952943     .034081198
   1.62931217         180.000000     .152641401     .033929475
   1.64560529         180.000000     .152271288     .034030406
   1.61464040         180.000000     .152924767     .034054374
   1.63094990         180.000000     .152606687     .033928436
   1.64725940         180.000000     .152230851     .034054143

Keep this file around, as we'll need it in a few minutes.

Finding E_i = E(V_i,(c/a)_i)

We now want to find the ``energy'' as a function of volume for this hcp lattice. By ``energy'', we mean ``lowest possible energy at this volume,'' and we determine this by the above procedure. Only now we'll do it for several volumes. Rather than bore you with all the calculations, I'll just leave the corresponding skeng files here and let you look at them. You can also run these calculations yourself using the qnewt script and the prototype SKIN file, skin.1. Save these files in your work/eos directory and you are ready to run. (If you are impatient, use the script qnewt3, which runs three iterations at a time.)

After calculations at several volumes, I now have a collection of skeng files:

$ cd work/eos
$ ls -l skeng.*
-rw-r-----   1 mehl     users         567 Jun  4 10:43 skeng.150
-rw-r-----   1 mehl     users         567 Jun  4 10:19 skeng.160
-rw-r-----   1 mehl     users         567 Jun  4 10:22 skeng.170
-rw-r-----   1 mehl     users         567 Jun  4 10:07 skeng.180
-rw-r-----   1 mehl     users         567 Jun  4 10:26 skeng.190
-rw-r-----   1 mehl     users         567 Jun  4 10:28 skeng.200
-rw-r-----   1 mehl     users         567 Jun  4 10:34 skeng.210
-rw-r-----   1 mehl     users         567 Jun  4 10:36 skeng.220
-rw-r-----   1 mehl     users         567 Jun  4 10:37 skeng.230
-rw-r-----   1 mehl     users         567 Jun  4 10:38 skeng.238
-rw-r-----   1 mehl     users         567 Jun  4 10:39 skeng.240
-rw-r-----   1 mehl     users         567 Jun  4 10:40 skeng.250
-rw-r-----   1 mehl     users         567 Jun  4 10:41 skeng.260

We know that the each skeng file contains the minimum energy found at the volume, so we can use the script work/eos/findmin to sort through each file, find the c/a ratio containing the lowest energy, and send this line to the file work/eos/hcp.eng:

$ cat hcp.eng
   1.64497271         150.000000     .195912899     .187430852
   1.64184610         160.000000     .177130438     .114704213
   1.63673261         170.000000     .163199291     .066240831
   1.63094990         180.000000     .152606687     .033928436
   1.62572142         190.000000     .144411879     .012838414
   1.62101427         200.000000     .137941785    -.000118739
   1.61695142         210.000000     .132735107    -.006950248
   1.61328739         220.000000     .128506077    -.009018008
   1.60960698         230.000000     .125062415    -.007287369
   1.60658379         238.000000     .122770055    -.003661979
   1.60579146         240.000000     .122252758    -.002485065
   1.60174402         250.000000     .119954645     .004811185
   1.59771104         260.000000     .118069641     .014124605

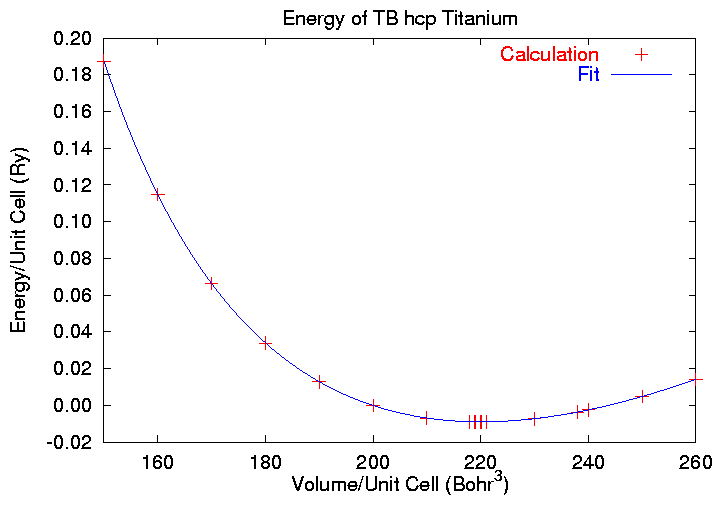
The minimum energy volume is near 220 Bohr³, somewhat smaller than experiment but fairly consistent with first-principles results. You'll note, though, that the equilibrium c/a ratio is nowhere near the experimental value of 1.586. This is an error in our tight-binding parametrization. We are considering improvements in the parametrization which will improve the calculated c/a value.

Finding the Equation of State and Equilibrium Properties

Now that we have a file containing E(V), we can use a Birch fit to find the equilibrium energy and bulk modulus. This is most easily done with a gnuplot script, work/eos/hcpfit.gnu, which fits the total energy to a third-order Birch polynomial. Running this script we get

$ gnuplot hcpfit.gnu
[Fitting Information Deleted]
Equilibrium Volume = 218.825567968325 Bohr^3 = 32.426610660628 Angstroms^3
Equilibrium Energy = -0.00892653034413964 Ry
Equilibrium Bulk Modulus = 0.00821086196105331 Ry/Bohr^3 = 120.786019536211 GPa
dB/dP (P=0) = 5.26167550134072
Press Enter to end program
$

Unfortunately, the predicted equilibrium energy is higher than the known energy at V=220 Bohr³, so we have to search around for the minimum a bit. Eventually we come up with an equilibrium volume of 220.088 Bohr³, and the file work/eos/hcp.eng:

   1.64497271         150.000000     .195912899     .187430852
   1.64184610         160.000000     .177130438     .114704213
   1.63673261         170.000000     .163199291     .066240831
   1.63094990         180.000000     .152606687     .033928436
   1.62572142         190.000000     .144411879     .012838414
   1.62101427         200.000000     .137941785    -.000118739
   1.61695142         210.000000     .132735107    -.006950248
   1.61400746         218.000000     .129283772    -.008934964
   1.61372104         218.800000     .128968824    -.008986750
   1.61364943         219.000000     .128890893    -.008995800
   1.61328739         220.000000     .128506077    -.009018008
   1.61326030         220.088000     .128472502    -.009018141
   1.61293422         221.000000     .128128916    -.009002417
   1.60960698         230.000000     .125062415    -.007287369
   1.60658379         238.000000     .122770055    -.003661979
   1.60579146         240.000000     .122252758    -.002485065
   1.60174402         250.000000     .119954645     .004811185
   1.59771104         260.000000     .118069641     .014124605

So, using our new equilibrium volume of 220.088 Bohr³ and equilibrium energy of -0.009018141 Ry, we can do a higher-order Birch fit using the script work/eos/hcpfit2.gnu . This gives us the information:

$ gnuplot hcpfit2.gnu
Fit set for vo = 220.088 Bohr^3 and
Eo = -0.009018141 Ry.  Change hcpfit2.gnu if necessary.
Press Enter to continue
[Fitting Information Deleted]
Equilibrium Volume = 220.088 Bohr^3 = 32.613683827428 Angstroms^3
Equilibrium Energy = -0.009018141 Ry
Equilibrium Bulk Modulus = 0.00827546824166049 Ry/Bohr^3 = 121.736411286626 GPa
dB/dP (P=0) = 3.80824655679457
Press Enter to end program
$

and the plot:

So to summarize this section, we've found the following:

	Experiment	First-Principles	Tight-Binding
a₀	5.575 Bohr = 2.95 Å	5.424 Bohr = 2.87 Å	5.400 Bohr = 2.858 Å
c₀	8.844 Bohr = 4.68 Å	8.598 Bohr = 4.55 Å	8.715 Bohr = 4.611 Å
V₀	238.0 Bohr³ = 35.27 Å³	219.1 Bohr³ = 32.46 Å³	220.088 Bohr³ = 32.614 Å³
(c/a)₀	1.586	1.585	1.613
B₀	105 GPa	120 GPa	121.7 GPa

Go back to the Example X home page.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

static Home Page Introduction About Version 1.11 Installation List of Files Usage Input Files Output Files Trouble Shooting Appendix