Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example X

Orthorhombic strain to find C₁₁-C₁₂

Computational Procedure

Go back to the theory

On the previous page we discovered that in order to determine C₁₁-C₁₂ in a hcp lattice we needed to strain the crystal so that the primitive vectors become

We need to follow the same basic procedure as in the EOS calculation:

1. Fix x
2. Find the value of u = u_min which minimizes E(x,u) at that value of x and determine an energy E(x)=E(x,u_min)
3. Use these E(x) to determine the elastic constant from the relationship

   E(x) = E₀ + V₀ (C₁₁-C₁₂) x² + O[x³]   .     (4)

To run the calculation, we need the spacegroup file work/c11-c12/spcgp1.63 . This is not quite the same as the corresponding space group file for the B33 lattice because we are using a different set of primitive vectors. We also need a k-point mesh. Again, as for the previous calculations in this section, we can save a lot of time by determining the k-point mesh once and for all. We do this by the same means as for the true hcp lattice, only using the lower symmetry space group file for Cmcm, work/c11-c12/spcgp1.63. The resulting k-point mesh contains 637 points and is stored in work/c11-c12/kmesh.63 .

The remaining procedure pretty much follows the work in finding the EOS. We need

1. A prototype SKIN file work/c11-c12/skin.1 ; which is used by
2. a script work/c11-c12/umin which takes values of x and u as input, and returns a value of u closer to the minimum energy structure for the current value of x (along with work/c11-c12/umin3 for the impatient);
3. a script work/c11-c12/findmin which finds the lowest energy for every value x, and puts all of this into a file work/c11-c12/c11-c12.eng ; and finally
4. a gnuplot script work/c11-c12/c11-c12fit.gnu which fits E(x) to (4) and determines the elastic constant C₁₁-C₁₂.

The examples follow the EOS work, so I won't go through them here. You can look in the directory work/c11-c12 for the results. In particular, look at the file work/c11-c12/skeng.0.0000 to see the limitations of this method.

Finally, we get the energy file work/c11-c12/c11-c12.eng , which looks like this:

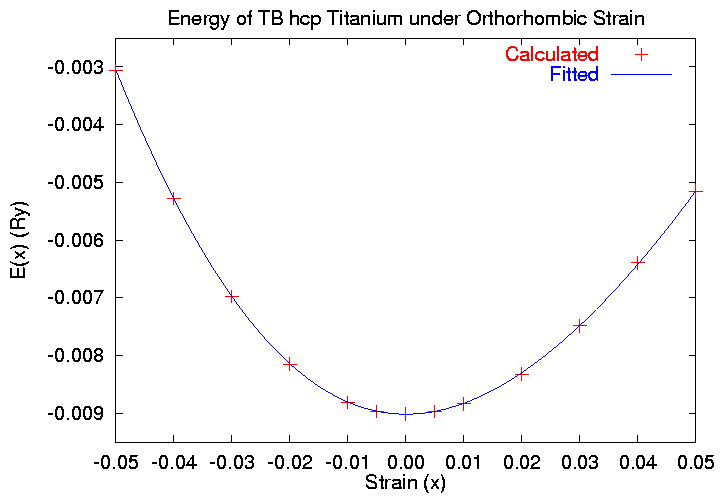
-0.0500  0.007530876  220.088000     .123181890    -.003061492
-0.0400  0.006483847  220.088000     .124775419    -.005282802
-0.0300  0.005160538  220.088000     .126205172    -.006979316
-0.0200  0.003693353  220.088000     .127352993    -.008151138
-0.0100  0.002037456  220.088000     .128157175    -.008814712
-0.0050  0.001071564  220.088000     .128389330    -.008969137
0.0000  0.000000000   220.088000     .128472502    -.009018141
0.0050 -0.001159830   220.088000     .128384019    -.008972413
0.0100 -0.002337862   220.088000     .128120487    -.008839575
0.0200 -0.004609668   220.088000     .127145485    -.008322533
0.0300 -0.006843999   220.088000     .125709107    -.007487313
0.0400 -0.009060559   220.088000     .123926395    -.006397543
0.0500 -0.011319330   220.088000     .121940516    -.005153007

Using the fitting/plotting routine work/c11-c12/c11-c12fit.gnu we get:

$ gnuplot c11-c12fit.gnu 
Using vo = 220.088 eo = -0.009018141
Edit c11-c12fit.gnu if necessary
Press  to continue
[Delete fitting information.  See work/c11-c12/fit.log for details
C_{11}-C_{12} = 133.531675480411 GPa
Press  to quit

So in summary, in this section we found

C₁₁ - C₁₂ = 133.5 GPa

Go back to the theory.

Go back to the Example X home page.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

Return to the static Reference Manual.