Last Modified 17 December 1999

The ``Static'' Tight-Binding Program: Example X

Change in energy as a function of a at fixed c

So far we've looked at the energy of the hcp Titanium lattice as a function of

• volume at fixed c/a and
• c/a at fixed volume

It turns out that there is. In this section we'll take a look at the effects of changing the lattice constant a while leaving c fixed. In the next section we'll change c and keep a fixed.

As usual, the change in one of the lattice parameters of the hcp crystal is related to an elastic constant. If we change the lattice constant a, say by

a ---> a' = a (1 + x)   ,     (1)

then according to our elastic constant tutorial we've constructed a strain

e₁ = e₂ = x   ;   e_3-6 = 0   .     (2)

This leads to the energy-strain relationship

E(x) = E₀ + V₀ (C₁₁ + C₁₂) x² + O[x³]     (3)

By now the drill should be pretty familiar: calculate E(x) at several points x, and determine the the elastic constant from a polynomial fit to the data. We'll do this in the directory work/c11+c12. The only tricky thing to note is that the pre-defined strain types table does not have an entry for the strain (2), so we'll have to use option ``1'' and provide all six of the e_i. Thus the first calculation in the work/c11+c12/SKIN file looks like this:

Mode=3               (Calculate energy only -- no pressure)
0.005  0.500         (T_{Fermi}, Eigenvalue cutoff for P calculation)
../ti_par
Titanium HCP (A3) -- Fixed c
 1.61326030 -0.050   (We'll use the label to indicate c/a and strain)
 0.00                (Electrons in addition to nominal Ti charge (=4/atom))
-3                   (hexagonal lattice, read in V and c/a)
 220.088  1.61326030 (V in Bohr^3 and c/a)
 1                   (General strain)
-0.050 -0.050 0 0 0 0   (the strain factors)
 2                   (Atoms in the unit cell)
 4 4 4               (Neighbor search cutoff indices)
F                    (Logical variable -- no internal displacements)
1 0.33333333333333333 0.66666666666666667 0.25 0 0 0   (Atom 1 in lattice coord.)
1 0.66666666666666667 0.33333333333333333 0.75 0 0 0   (Atom 2 in lattice coord.)
NEWSYM=T             (Generate new set of k-points)
LATTIC=4             (Lattice type / Next is spacegroup file name:)
../spcgp1.hcp
ILAT=T               (Space group file in lattice Coordinates)
-1313                (Read k-point generation information from file)
../kmesh.194

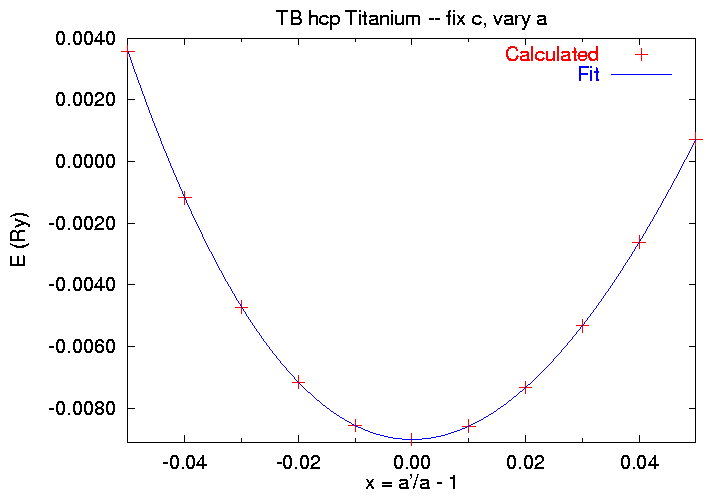
We use strain option 1, so we have to specify all six e_i, according to (2). When we run the code for a full set of strains, we find

$ cat SKENG
 1.61326030 -0.050    198.629420     .136781884     .003566595
 1.61326030 -0.040    202.833101     .134873918    -.001177001
 1.61326030 -0.030    207.080799     .133110223    -.004722904
 1.61326030 -0.020    211.372515     .131464657    -.007158055
 1.61326030 -0.010    215.708249     .129921976    -.008564840
 1.61326030  0.000    220.088000     .128472502    -.009018141
 1.61326030  0.010    224.511769     .127108770    -.008586483
 1.61326030  0.020    228.979555     .125823896    -.007336256
 1.61326030  0.030    233.491359     .124610983    -.005327283
 1.61326030  0.040    238.047181     .123461329    -.002622256
 1.61326030  0.050    242.647020     .122365654     .000721244

Note that it is much more difficult to compress the lattice than to expand it. We'll use a modification of the fitting procedure we used in the fixed volume case, using gnuplot to fit this data to the polynomial

E(x) = E₀ + V₀ x² [ (C₁₁ + C₁₂) + x ( A + x ( B + x C))]   ,   (4)

where A, B, and C are higher order elastic constants. When we run the fitting script we get

$ gnuplot caafit.gnu  
Starting from v0 = 220.088 and e0 = -0.009018141
Change if appropriate
Press  to continue
[Fitting information deleted.  See fit.log]
C_{11} + C_{12} = 295.490246436718 GPa
Press  to quit
$

So in this section we've found that

Go back to the Example X home page.

Look at other examples.

Get other parameters from the Tight-binding periodic table.

Return to the static Reference Manual.