Last updated -- 17 December 1999

The ``Static'' Tight-Binding Program: The Output

This page shows how to interpret the results of a run of the static Tight-Binding program.

To run the code you will need several files:

  1. The tight-binding parameters
  2. The space group files for your lattices
  3. The k-point files for these lattices
  4. The input file for the Static program, named "SKIN".

The first setup page has the information you need to find the first three files. The second setup page details the construction of the SKIN file.

Your working directory should now look something like this: 

$ls -l
total 47
-rw-r--r--   2 mike     mike        11634 May 25 11:21 SKIN
-r--r--r--   2 mike     mike         2410 Jun  2  1995 bcc.08
-r--r--r--   2 mike     mike         3468 Jun  1  1995 fcc.08
-r--r--r--   2 mike     mike         7162 May 25 11:00 pd_par
-r--r--r--   2 mike     mike        10003 Aug 15  1996 spcgrp.bcc
-r--r--r--   2 mike     mike        10003 Jul 28  1997 spcgrp.fcc

The static program reads the SKIN, parameter, k-point and space group files and produces three types of output:

  1. Standard output, which simply allows you to chart the progress of the program
  2. A detailed SKOUT file, which reprints the primitive vectors and the atomic positions, so that you can check your input.
  3. The SKENG file, which we'll discuss below.

The SKENG file should look like this (I've edited out some of the spaces for clarity): 

 fcc  6.80   78.608000   .256797277   .038518611   .004624940
 fcc  6.90   82.127250   .242276268   .024020018   .003607059
 fcc  7.00   85.750000   .228826554   .012851841   .002567833
 fcc  7.10   89.477750   .216099374   .005144880   .001585545
 fcc  7.20   93.312000   .203907640   .000802042   .000703127
 fcc  7.30   97.254250   .192381931  -.000433135  -.000048809
 fcc  7.40  101.306000   .181915501   .001011535  -.000625782
 fcc  7.50  105.468750   .172358630   .004490358  -.001055989
 fcc  7.60  109.744000   .163145676   .009793201  -.001410457
 bcc  5.30   74.438500   .260259224   .075705141   .006146868
 bcc  5.40   78.732000   .242412877   .051649155   .004989744
 bcc  5.50   83.187500   .225463671   .032543604   .003583378
 bcc  5.60   87.808000   .209785142   .019214376   .002215440
 bcc  5.70   92.596500   .195912039   .011547488   .001040896
 bcc  5.80   97.556000   .184151847   .008633127   .000166792
 bcc  5.90  102.689500   .173251125   .009740659  -.000557775
 bcc  6.00  108.000000   .163646043   .014154297  -.001067757
 bcc  6.10  113.490500   .155520444   .020906271  -.001364898

  1. The first 20 characters of each line contain the labels we entered into the SKIN file. Since we entered the lattice type and the lattice constant this takes up two columns.
  2. The next column holds the volume of the unit cell for the lattice, in atomic units.
  3. The next column shows the Fermi level, in Rydbergs. The energy zero for the band structure is set by the parametrization.
  4. The next column, which will be the last column if you run with Mode = 3, is the energy of this lattice, in Rydbergs (1 Rydberg = 13.6056981 eV). Again, the energy zero is set by the program, but it is the same zero for all structures using this parameter file, so you can easily compare energies between different structures.
  5. The final column contains the pressure, which is calculated only for Mode = 4. This is in the natural units of the program, Rydbergs/a.u.3, where 1 Rydberg/a.u.3 = 14710.5164 GPa, or 147.105164 MBar. Of course, we can use the pressure to determine the equilibrium lattice constant. In this example we see that the fcc equilibrium is between 7.2 and 7.3 a.u., and the bcc equilibrium is between 5.8 and 5.9 a.u.

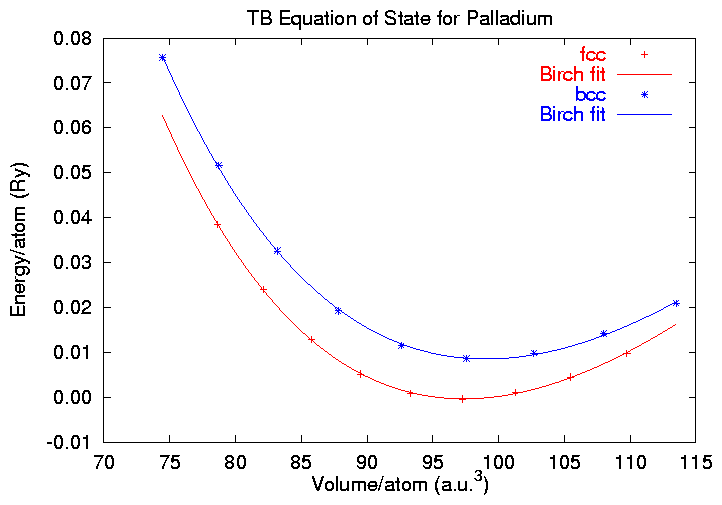
An easy way to visualize these results uses the free program gnuplot. If we use the 3.7 version, we can even use its fitting routines to make a Birch fit to the fcc and bcc data, which will allow us to obtain the equilibrium lattice constants and bulk moduli for the two phases. Using the gnuplot script pdfit.gnu we get the output 

$ gnuplot pdfit.gnu
[Fitting routine information deleted, see fit.log]
Results of 3rd order Birch fit:
FCC Lattice:
E_0 = -0.000386492440903136 Ry
V_0 = 97.3474098780412 Bohr**3
a_0 = 7.30233014694192 Bohr
B_0 = 231.411489521339 GPa
B_0'= 3.55235088090646
BCC Lattice:
E_0 = 0.00848554898771665 Ry
V_0 = 99.0135973207143 Bohr**3
a_0 = 5.82874351166457 Bohr
B_0 = 217.013641667665 GPa
B_0'= 3.39317618244097
FCC - BCC energy diference = 0.120710317208493 eV
Using the GIF driver available with gnuplot, we produce the following result:
E(V) for fcc and bcc Pd
You can also use the enhanced postscript driver to make a printable plot. pdfit.gnu also saves its results in the script pdplot.gnu, which you can use to make a prettier presentation plot.

Return to the first setup page

Go back to the second setup page

Look at other examples.

static Home Page   Introduction   About Version 1.11   Installation   List of Files   Usage   Input Files   Output Files   Trouble Shooting   Appendix

Return to the static Reference Manual.